3D-s számítógépes geometria és alakzatrekonstrukció

A Bézier és B-spline görbék kiértékelése

http://cg.iit.bme.hu/portal/node/312
https://portal.vik.bme.hu/kepzes/targyak/VIIIMA25

Dr. Várady Tamás, Dr. Salvi Péter
BME, Villamosmérnöki és Informatikai Kar
Irányítástechnika és Informatika Tanszék

Tartalom

• Bézier görbék
  • Kiértékelés
  • Deriváltszámítás
• B-Spline görbék
  • Kiértékelés
  • Deriváltszámítás
• NURBS (racionális B-Spline görbék)
  • Kiértékelés
  • Deriváltszámítás

[Irodalom: Piegl, Tiller: The NURBS Book]

Bézier görbék (ismétlés)

• Vektorpolinom:
• Kontrollpontokhoz intuitív jelentés
• Fokszám = Kontrollpontok száma – 1
• Bernstein polinomok:

Reprezentáció

// Vector típus a szokásos műveletekkel
#include "vector.hh"

using Point        = Vector;
using PointVector  = std::vector<Point>;
using VectorVector = std::vector<Vector>;
using DoubleVector = std::vector<double>;
using DoubleMatrix = std::vector<DoubleVector>;
using PointMatrix  = std::vector<PointVector>;

struct BezierCurve
{
  size_t n;                     // fokszám => n + 1 kontrollpont
  PointVector cp;               // kontrollpontok

  // ...                        // member függvények
};

Kiértékelés – közvetlen módszer

• A képlet kibontva:

• Probléma:
  • Bonyolult görbe → magas fokszám (vö. BSpline)
  • Numerikusan instabil
• Pl.:
  • esetén =
• Nem használható (kivéve ha kicsi)

Stabil Bernstein kiértékelés

• Megoldás: rekurziós képlet:

• Kezdőérték:
  • Nulladfokúnál
  • Az "érdekes" háromszög -dik eleme
• A háromszög egy oszlopát tároljuk
• Balról jobbra haladunk

Stabil Bernstein kiértékelés

double BezierCurve::bernstein(size_t i, size_t n, double u)
{
  DoubleVector tmp(n + 1, 0.0);
  tmp[n-i] = 1.0;
  double u1 = 1.0 - u;
  for (size_t k = 1; k <= n; ++k)
    for (size_t j = n; j >= k; --j)
      tmp[j] = tmp[j-1] * u + tmp[j] * u1;
  return tmp[n];
}

Point BezierCurve::evaluateOneByOne(double u) const
{
  Point p(0.0, 0.0, 0.0);
  for (size_t k = 0; k <= n; ++k)
    p += cp[k] * bernstein(k, n, u);
  return p;
}

Hatékonyabb kiértékelés

• Külön háromszög minden Bernstein polinomhoz → nem hatékony
• Egy háromszögből kijön mindegyik
• Trükk: fordított irány
• A háromszögön kívül levő értékek 0-k
• Balról jobbra, felülről lefele
• Plusz változó mentéshez

Hatékonyabb kiértékelés

void BezierCurve::bernsteinAll(size_t n, double u, DoubleVector &coeff)
{
  coeff.clear(); coeff.reserve(n + 1);
  coeff.push_back(1.0);
  double u1 = 1.0 - u;
  for (size_t j = 1; j <= n; ++j) {
    double saved = 0.0;
    for (size_t k = 0; k < j; ++k) {
      double tmp = coeff[k];
      coeff[k] = saved + tmp * u1;
      saved = tmp * u;
    }
    coeff.push_back(saved);
  }
}

Hatékonyabb kiértékelés

Point BezierCurve::evaluate(double u) const
{
  DoubleVector coeff; bernsteinAll(n, u, coeff);
  Point p(0.0, 0.0, 0.0);
  for (size_t k = 0; k <= n; ++k)
    p += cp[k] * coeff[k];
  return p;
}

Point BezierCurve::
evaluateWithCachedCofficients(const DoubleVector &coeff) const
{
  Point p(0.0, 0.0, 0.0);
  for (size_t k = 0; k <= n; ++k)
    p += cp[k] * coeff[k];
  return p;
}

A de Casteljau algoritmus

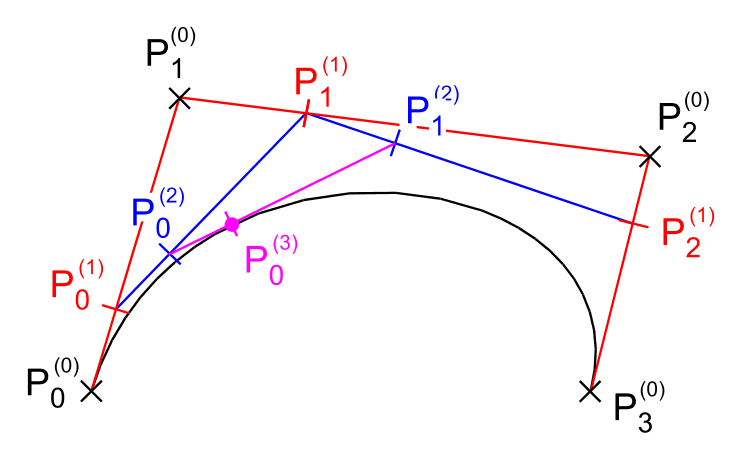
• Kontrollpontok lemásolása
• Következő poligon kiszámolása
• Egyre rövidebb
  • Egy pont marad, ez a görbepont

A de Casteljau algoritmus

Point BezierCurve::evaluateByDeCasteljau(double u) const
{
  PointVector tmp = cp;
  double u1 = 1.0 - u;
  for (size_t k = 1; k <= n; ++k)
    for (size_t i = 0; i <= n - k; ++i)
      tmp[i] = tmp[i] * u1 + tmp[i+1] * u;
  return tmp[0];
}

• Egyszerű
• Lassú
  • Műveletek pontokkal és nem számokkal
  • Nem cache-elhető

Összehasonlítás

• Pontosság azonos (kivéve a közvetlen kiértékelést)
• 100-adfokú görbe kiértékelése 100 pontban 100x (2.8GHz CPU)

(*) beleértve a cache-elést is

Bézier deriváltak (ismétlés)

Deriváltszámítás

• A -adik derivált kontrollpontjaihoz kellenek a -edik kontrollpontjai
• Érdemes az összes deriváltat kiszámítani
• Szükséges:
  • Kontrollpontok minden deriválthoz
  • Bernstein polinomok minden fokszámhoz
    (ezt is érdemes egyszerre kiszámítani)
  • Deriváltszámítás, figyelve a esetre

Kontrollpontok minden deriválthoz

// Feltételezi, hogy d <= n
void BezierCurve::derivativeControlPoints(size_t d, PointMatrix &dcp) const
{
  dcp.clear(); dcp.resize(d + 1);
  dcp[0] = cp;
  for (size_t k = 1; k <= d; ++k) {
    size_t tmp = n - k + 1;
    dcp[k].reserve(tmp);
    for (size_t i = 0; i <= n - k; ++i)
      dcp[k].push_back((dcp[k-1][i+1] - dcp[k-1][i]) * tmp);
  }
}

Bernstein polinomok minden fokszámhoz

void BezierCurve::bernsteinAll(size_t n, double u, DoubleMatrix &coeff)
{
  coeff.clear(); coeff.resize(n + 1);
  coeff[0].push_back(1.0);
  double u1 = 1.0 - u;
  for (size_t j = 1; j <= n; ++j) {
    coeff[j].reserve(j + 1);
    double saved = 0.0;
    for (size_t k = 0; k < j; ++k) {
      double tmp = coeff[j-1][k];     // ... = coeff[k]  helyett
      coeff[j].push_back(saved + tmp * u1); // coeff[k] = ...  helyett
      saved = tmp * u;
    }
    coeff[j].push_back(saved);
  }
}

Deriváltszámítás

Point BezierCurve::
derivativesByControlPoints(double u, size_t d, VectorVector &der) const
{
  size_t du = std::min(d, n);
  der.clear(); der.reserve(d + 1);
  DoubleMatrix coeff; bernsteinAll(n, u, coeff);
  PointMatrix dcp; derivativeControlPoints(du, dcp);
  for (size_t k = 0; k <= du; ++k) {
    der.emplace_back(0.0, 0.0, 0.0);
    for (size_t j = 0; j <= n - k; ++j)
      der[k] += dcp[k][j] * coeff[n-k][j];
  }
  for (size_t k = n + 1; k <= d; ++k)
    der.emplace_back(0.0, 0.0, 0.0);
  return der[0];
}

• Vektorműveletek - jobb lenne a Bernstein deriváltjából számolni
  • De ennek mintájára egyszerűbb B-spline derivált

BSpline görbék (ismétlés)

• Polinomiális szakaszokból álló görbe
• A szakaszok azonos fokszámúak ()
• Paraméterezés csomóvektorral
  • Monoton növekvő számsorozat
  • Multiplicitás csökkenti a folytonosságot
  • -szeres multiplicitás interpolál
  • → Bézier görbe
    ( ill. multiplicitása a görbe rendje)
• Lokális; szűkebb konvex burok

BSpline görbék (kitérő)

• Máshogy: -edfokú Bézier görbék sorozata
  • Csatlakozásnál folytonossági feltétel
  • Csak a nem triviális kontrollpontok kellenek
  • Szimmetrikusan választjuk ki
  • A polárkoordinátákból megkapjuk a csomóvektort

BSpline bázis (ismétlés)

Reprezentáció

struct BSplineCurve
{
  size_t p;                     // fokszám
  size_t n;                     // n + 1 = cp.size()
  DoubleVector knots;           // első és utolsó p+1 érték megegyezik (*)
  PointVector cp;               // knots.size() = cp.size() + p + 1

  // ...                        // member függvények
};

// (*) Biztosítja a végpont-interpolációt

A bázisfüggvények kiszámítása

• Adott u-nál melyik bázisfüggvények élnek?

• Ezeket érdemes egyszerre kiszámolni
  • Bernstein polinomokhoz hasonlóan fordított irányban háromszögépítés
• pl.: , ,

size_t BSplineCurve::findSpan(double u) const
{
  // Külön kell kezelni az intervallum végét
  if (u >= knots[n+1])
    return n;
  return (std::upper_bound(knots.begin() + p + 1,
                           knots.end(), u)
          - knots.begin()) - 1;
}

A bázisfüggvények kiszámítása

// knots = {0,..,0,1,...,1} => bernstein
void BSplineCurve::
basisFunctions(size_t i, double u, DoubleVector &coeff) const
{
  coeff.clear(); coeff.reserve(p + 1);
  coeff.push_back(1.0);
  DoubleVector left(p + 1), right(p + 1); // 0. elem nincs kihasználva
  for (size_t j = 1; j <= p; ++j) {
    left[j]  = u - knots[i+1-j];
    right[j] = knots[i+j] - u;
    double saved = 0.0;
    for (size_t r = 0; r < j; ++r) {
      double tmp = coeff[r] / (right[r+1] + left[j-r]);
      coeff[r] = saved + tmp * right[r+1];
      saved = tmp * left[j-r];
    }
    coeff.push_back(saved);
  }
}

BSpline kiértékelés

• Bázisfüggvények alapján:

Point BSplineCurve::evaluate(double u) const
{
  double span = findSpan(u);
  DoubleVector coeff; basisFunctions(span, u, coeff);
  Point point(0.0, 0.0, 0.0);
  for (size_t i = 0; i <= p; ++i)
    point += cp[span - p + i] * coeff[i];
  return point;
}

• Alternatíva: de Boor algoritmussal
  • A de Casteljau algoritmus általánosítása
  • Csomóbeszúrás addig, amíg -szer benn nem lesz
• A két algoritmus kb. ugyanolyan gyors

A de Boor algoritmus

• Kell: multiplicitás számítás

size_t BSplineCurve::findSpanWithMultiplicity(double u, size_t &multi) const
{
  auto range = std::equal_range(knots.begin(), knots.end(), u);
  multi = range.second - range.first;

  if (u >= knots[n+1])
    return n;
  return (range.second - knots.begin()) - 1;
}

• Új kontrollpont-pozíciók:
  ahol

A de Boor algoritmus

• Csak a lényeges pontokat számoljuk

Point BSplineCurve::evaluateByKnotInsertion(double u) const
{
  if (u <= knots[0])
    return cp[0];
  if (u >= knots[n+p+1])
    return cp[n];
  size_t s, k = findSpanWithMultiplicity(u, s), r = p - s;
  PointVector tmp; tmp.reserve(r + 1);
  std::copy_n(cp.begin() + k - p, r + 1, std::back_inserter(tmp));
  for (size_t j = 1; j <= r; ++j)
    for (size_t i = 0; i <= r - j; ++i) {
      double alpha = (u - knots[k-p+j+i]) / (knots[i+k+1] - knots[k-p+j+i]);
      tmp[i] = tmp[i+1] * alpha + tmp[i] * (1.0 - alpha);
    }
  return tmp[0];
}

BSpline deriváltak

• A Bézier görbékhez hasonlóan:

Deriváltszámítás

• Érdemes az összes deriváltat kiszámítani
• Szükséges:
  • Kontrollpontok minden deriválthoz (csak amik a pont környékén vannak)
  • Bázisfüggvények minden fokszámhoz (ezt is érdemes egyszerre kiszámítani)
  • Deriváltszámítás, figyelve a esetre
• Teszt: , , 100 mintapont 100x
• 2 derivált kiértékelés (2.8GHz CPU): 0.1s
• Bázisfüggvények deriváltjaival is lehet
  • Bonyolultabb, nem lényegesen gyorsabb

BSpline deriváltak kontrollpontjai

// Feltételezi, hogy d <= p
// Csak az [r1, r2] kontrollpont-intervallumra számolja ki
void BSplineCurve::derivativeControlPoints(size_t d, size_t r1, size_t r2,
                                           PointMatrix &dcp) const
{
  dcp.clear(); dcp.resize(d + 1);
  size_t r = r2 - r1;
  dcp[0].reserve(r + 1);
  for (size_t i = 0; i <= r; ++i)
    dcp[0].push_back(cp[r1+i]);
  for (size_t k = 1; k <= d; ++k) {
    dcp[k].reserve(r + 1 - k);
    size_t tmp = p - k + 1;
    for (size_t i = 0; i <= r - k; ++i)
      dcp[k].push_back((dcp[k-1][i+1] - dcp[k-1][i]) * tmp /
                       (knots[r1+i+p+1] - knots[r1+i+k]));
  }
}

Az összes bázisfügvény

void BSplineCurve::basisFunctionsAll(size_t i, double u,
                                     DoubleMatrix &coeff) const
{
  coeff.clear(); coeff.resize(p + 1);
  coeff[0].push_back(1.0);
  DoubleVector left(p + 1), right(p + 1);
  for (size_t j = 1; j <= p; ++j) {
    coeff[j].reserve(j + 1);
    left[j]  = u - knots[i+1-j];
    right[j] = knots[i+j] - u;
    double saved = 0.0;
    for (size_t r = 0; r < j; ++r) {
      double tmp = coeff[j-1][r] / (right[r+1] + left[j-r]);
      coeff[j].push_back(saved + tmp * right[r+1]);
      saved = tmp * left[j-r];
    }
    coeff[j].push_back(saved);
  }
}

Deriváltszámítás

Point BSplineCurve::derivativesByControlPoints(double u, size_t d,
                                               VectorVector &der) const
{
  size_t du = std::min(d, p);
  der.clear();
  size_t span = findSpan(u);
  DoubleMatrix coeff; basisFunctionsAll(span, u, coeff);
  PointMatrix dcp; derivativeControlPoints(du, span - p, span, dcp);
  for (size_t k = 0; k <= du; ++k) {
    der.emplace_back(0.0, 0.0, 0.0);
    for (size_t j = 0; j <= p - k; ++j)
      der[k] += dcp[k][j] * coeff[p-k][j];
  }
  for (size_t k = p + 1; k <= d; ++k)
    der.emplace_back(0.0, 0.0, 0.0);
  return der[0];
}

Racionális görbék (ismétlés)

• Racionális BSpline (NURBS) görbe:

• Homogén koordináták:
• Vetítés a síkra:

NURBS kiértékelés

• Plusz koordináta → magasabb dimenzió
  • Példa: 2D NURBS ( koordináta: )

Point BSplineCurve::evaluate2DRational(double u) const
{
  Point p = evaluate(u);
  return Point(p.x / p.z, p.y / p.z, 1.0);
}

NURBS deriváltak

NURBS deriváltak

Point BSplineCurve::derivatives2DRational(double u, size_t d,
                                          VectorVector &der) const
{
  der.clear(); der.reserve(d + 1);
  VectorVector der3d; derivativesByControlPoints(u, d, der3d);
  for (size_t k = 0; k <= d; ++k) {
    Vector v = der3d[k];
    for (size_t i = 1; i <= k; ++i)
      v = v - der[k-i] * der3d[i].z * binomial(k, i);
    der.push_back(v / der3d[0].z);
  }
  return der[0];
}

Binomiális együtthatók

size_t BSplineCurve::binomial(size_t n, size_t k)
{
  if (k > n)
    return 0;
  size_t result = 1;
  for (size_t d = 1; d <= k; ++d, --n)
    result = result * n / d;
  return result;
}